Исходя из
принципов обратимости
процессов и круговорота
энергии в природе, Ф.Энгельс,
К.Э.Циолковский, Ю.Р.Мейер, Г.Л.М.
Гельмгольц, В.Ф.Г. Нернст,
П.Базаров, П.К.Ощепков и др.
отрицали “тепловую” смерть
Вселенной”, вытекающую из
закона возрастания энтропии D
Sі0 (Р.Клаузиус, В.Томпсон) и
согласующуюся с теософскими
бреднями о “начале” и
“конце” света.
Закон возрастания энтропии
приобрел характер “истины в
последней инстанции” после
того, как Л.Больцман и М.Планк
связали его с
термодинамической
вероятностью W=Nі1
S=klnWі0 (1)
В теории информации введена
отрицательная энтропия
(негэнтроприя — Л.Бриллюэн,
Р.Хартри, Л.Сциллард, К.Шеннон и
др., присуждена нобелевская
премия за 1977 г. И.Пригожину за
доказательство существования
устойчивых структур (в химии,
биологии) с отрицательной
энтропией. Однако
вышеназванные ученые не смогли
опровергнуть всеобщность
закона возрастания энтропии
(это показал К.Ребане) и формулы
(1), ссылки см. в [22].
Попытка опровержения
всеобщности закона DSі0
и (1) сделана в [22] на основе
ревизии основ термодинамики.
Утверждается [22], что так как
первое начало термодинамики (в
дифференциальной форме для m=m
):
dS=dU+dA=CvdT+PdV (2)
— следствие закона
сохранения энергии, а второе
начало получается из 1–го
делением его на абсолютную
температуру Т (К.А.Путилов и [23])
dS=dQ/T=dU/T+dA/T=CvdT/T+RdV/V
(2)
то второе начало суть
критериальная — ( Т — в
энергетических единицах) форма
записи первого начала, т.е.
безразмерная форма закона
сохранения и изменения
энергии. Доказательство
справедливости вышесказанного
состоит и в существовании
основного управления
термодинамики (Гибс,
Гельмгольц и др):
TdS=dU+dA; -dU=-TdS+dA (3)
которое объединяет в себе
1–ое и II–ое начала. Далее в [1]
утверждается, что устойчивые
системы природы
характеризуются полной
(отрицательной En)
энергией, En=Eпот+Eкин и
соответственно полной
(внутренней) отрицательной
энергией (из (2) имеем):
dSn=-CvdT/T=-dQ/T+RdV/V=dSпот+dSкин
(4)
и отрицательной энтропией,
соответствующей потенциальной
(тепловой — -dQ/T=dSпот )
энергии; dSкин=RdV/V
Возьмем определенный (5) и
неопределенный (5`) интеграл от
основного уравнения (2):
S=CvlnT2/T1+RlnV2/V1 (5)
S=CvlnT+RlnV+S0; D S=S-S0=CvlnT+RlnV (5`)
В (5) — энтропия, а в (5`) и
изменение энтропии,
соответствующее изменению
тепловой (Q) энергии.
Учитывая, что из уравнения
Мейера для теплоемкостей
Cp=Cv+R, g =Cp/Cv, R/Cv+g-1
получим из (5) [22]:
S/Cv=lnT2/T1+(c-1)lnV2/V1;
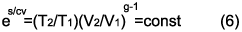
уравнение Пуассона. Для
случая изотермического (T2=T1
) процесса получим (7), а поделив
(7) на число Авогадро NA
- (7`):
S=Rln(V2/V1) (7);
Sm=kln(V2/V1) (7`)
где S и Sm
энтропии для одного моля газа и
молекулы. Заменив (1) отношением
V2/V1=N=W (V2>V1), получим (8)
закон возрастания энтропии для
процессов рассеяния и (8`) —
закон Больцмана–Планка:
S=RlnWі0 (8);
Sm=klnWі0 (8`)
а при отношении объемом V2/V1=1/N=P,
получим закон убывания
энтропии для процессов
концентрации [23]:
S=RlnPЈ0 (9);
Sm=klnPЈ0 (9`)
В (8,8`); (9,9`) W=N, P=1/N
суть термодинамическая (W)
и математическая (P)
вероятности (ln(1/N)=ln1-lnN=-lnW)
т.е. lnP=-lnW. В (9, 9`)
энтропии отрицательны. Наш
подход равнозначен введению
группы полной вероятности
(пусть W=10, P=1/10), тогда
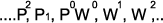 .: (10)
или для любого N: .: (10)
или для любого N:
..., P1, PW, W1, ...; ...lnP,
0, lnW, ... (10)
Группе полной вероятности (10)
соответствует закон
сохранения энергии S=0 для
циклического процесса в
технике и процессов пульсации
в природе:
RlnP, 0, RlnW; 0=Rln(P*W) (11)
Отметим, что (8,8`) и (9,9`)
соответствуют закону Бойля–
Мариотта PiVi=const; m,T=const,
при V2/V1=N=W, давление P2=1/N,
а при (9,9`) справедливо при
условии V2/V1=1/N=P,
давление P2=N. Так как
отношение объемов V2/V1=P1/P2
обратно отношению давлений
(примем, что V1=1, P1-1
суть объем и давление при
нормальных условиях, т.е. (P1=1aT,
T=273k, ln(V1/V1)=ln(P1/P1)=0)
логарифмируя, получим ln(V2/V1)=ln(P1/P2)
или ln(V2/V1)-ln(P1/P2)=0, иначе
при V2/V1=N=W, P2/P1=1/N=P
получим (lnN=-ln1/N)
lnW+lnP=0, RlnW+RlnP=0 (12)
в процессе расширения (за
счет работы растяжения) и
RlnP+RlnW=0 (12`)
в процессе сжатия. (12) и (12`)
суть запись закона
Бойля–Мариотта через
математическую (P) и
термодинамическую (W)
вероятность. В [22] приводится
аналогичная запись уравнения
Пуассона (6) для
адиабатического процесса.
Подробнее и ссылки см. в [22].
Забвение математической
вероятности привело
Больцмана– Планка к
чрезмерным обобщениям.
Введение математической
вероятности позволяет ввести
закон убывания энтропии D SЈ0. Из
закона сохранения полной
энергии Вселенной вытекает
закон сохранения полной
энергии Вселенной вытекает
закон сохранения полной
отрицательной энтропии
Вселенной. Рассеяние энергии
сопровождается возрастанием
энтропии, а концентрация — ее
убыванием. Модель постоянного
состояния (1940 г. Г.Бонди,
Т.Гоулд, Ф.Хойл) с постоянной
плотностью r =const
предполагает зарождение
вещества в звездах из мирового
эфира (вакуума). Поэтому
тепловая смерть Вселенной не
угрожает. Она не имеет ни
начала во времени, ни конца в
пространстве.
Заключение
Закон возрастания энтропии в
процессах рассеяния энергии
многими рассматривается как
один из важнейших законов
природы именно по той причине,
что, разрешая возрастание
энтропии (это очевидно), он
запрещает убывание энтропии
(что всегда вызывало сомнение).
Связь закона возрастания
энтропии с термодинамической
вероятностью (1) превратило
этот закон в “истину в
последней инстанции”.
Системный подход к проблеме
энтропии требует учета помимо
термодинамической и
математической вероятности.
Связав и термодинамическую и
математическую вероятность с
отношением объемов, которое
может быть больше единицы, и в
этом случае рассеяние энергии
сопровождается возрастанием
энтропии, и может быть меньше
единицы, в этом случае
применение математической
вероятности ведет к убыванию
энтропии в процессах
концентрации энергии. Из
закона сохранения энергии при
адиабатическом процессе
вытекает закон сохранения
энтропии, но это возможно
только если в полуцикле
концентрации энтропия убывает,
а в полуцикле рассеяния
энтропия возрастает. Для
уменьшения неопределенности и
путаницы в рассуждениях
следует применять
определенные интегралы вместо
обычно применяемых
неопределенных интегралов, в
этом случае во втором начале
термодинамики (см.5) получаем
отношение температур и
объемов, которые можно и нужно
заменять через математическую
и термодинамические
вероятности. В этом случае
закон убывания энтропии
вводится симметрично с законом
возрастания энтропии в
соответствии с системным
подходом.
БИБЛИОГРАФИЧЕСКИЙ
СПИСОК К ГЛ.1
1. Седов Л.И. Методы подобия и
размерности в механике Г.И.Т.–
ТЛ, М., 1954.
2. Веников В.А. Теория
подобия и моделирования. М.:
Высшая школа, 1966.
3, 4. Дидык Ю.К., Фигуровский Е.Н.
Курс лекций по физике, ч.1. НВИИ,
Норильск, 1975.
5, 6. Дидык Ю.К. Изв.вузов
“Физика”. Томск, 1964, N 1, с.9–17,
1965, N 6, с 14–22.
7, 8. Дидык Ю.К. Сб.трудов НВИИ.
Красноярск, N 4, с.3–46. Норильск,
1964, N 2, с.3–40.
9,10,11,12. Дидык Ю.К. Сб.трудов НВИИ.
Норильск, 1965, N 3, с.15–48.
Красноярск, 1970, N 7, с.5–28; 1969, N 5,
с.52–89 (соавторы: Спесивцев В.В.,
Ефимов М.И.), 1970, N 6, с.107–119.
13. Дидык Ю.К.
Физико–математическое
моделирование: Межвуз. и
межвед., сб. (НВИИ. Норильск, 1979,
с.3–20.
14. Дидык Ю.К. Гетерогенная
хемилюминисценция: Межвуз. и
межвед., сб. (НВИИ. Норильск, 1984,
с.115–122, 125–128.
15. Дидык Ю.К. и др. в кн.
“Система. Симметрия.
Гармония”. Изд. “Мысль”, 1988 г.
(под редакцией д.ф.н.:
В.С.Тюхтина, Ю.А.Урмандева).
16, 17. Кропоткин П.Н. Доклады АН
СССР, сер.матем.физика, 1971, 198. N 4,
с.798–800; 1972, 206, N 2, с.304–306.
18, 19. Дидык Ю.К. Физическое и
математическое моделирование
технических процессов НГМК:
Межвуз. и межвед., сб. (НВИИ.
Норильск, 1982, с.154–165. Там же,
с.166–169.
20, 21. Дидык Ю.К. Сб.трудов НВИИ N 2.
Физико– электротехнический
выпуск. Красноярское кн.изд.,
1964, с.3–28.
22. Дидык Ю.К. Закон убывания
и возрастания энтропии для
процессов концентрации и
рассеяния как следствие закона
сохранения полной энергии:
Межвуз. и межвед., сб. (НВИИ.
Норильск, 1985, с.94–102.
23. Дидык Ю.К., Фигуровский
Е.Н. Курс лекций по физике, ч.1
(НВИИ. Норильск, 1975, с.136.
|