ПРЕОБРАЗОВАНИЯ КООРДИНАТ

С.Н. Шмидт

Со времен Галилея, принцип относительности существует как незыблемый постулат механики. Но, что такое принцип относительности и можно ли ему доверять в эпоху космических полетов?

Математически принцип относительности Галилея сводится к преобразованию координат идеализированной системы отсчета, находящейся вне сферы действия гравитационных полей. При этом правильно утверждается, что, при выбранных условиях, за равные промежутки времени движущееся тело будет проходить равные отрезки в обеих системах отсчета.

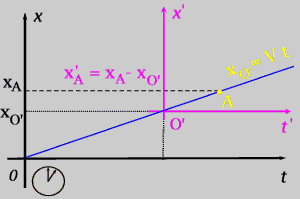
x_A' = x_A - x_O' = x_A - V·t; (1)

Dx' = |x_B' - x_A'| = |(x_B - V·t) - (x_A - V·t)| = Dx. (2)

Но другого результата в этом примере и не должно быть, так как отсутствуют силы и соответствующие им импульсы.

Возьмем два самолета, летящих с равными скоростями и посмотрим, как произойдет процесс посадки на палубу авианосца в неподвижной и движущейся системах отсчета.

Так как масса авианосца во много раз превышает массу самолета, то можно принять системы отсчета, связанные с неподвижным (относительно Земли) и движущимся авианосцами.

Рис.2

Рис.3 Рис.4

На Рис.3 происходит посадка на неподвижный авианосец, на Рис.4 - на движущийся.

Составим схему(Рис.5) и определим посадочный путь самолетов в различных системах отсчета при действии на них равных тормозных сил.

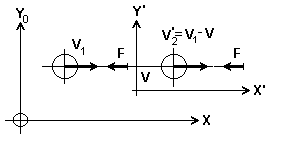
Рис.5

Тормозной путь первого самолета в неподвижной системе отсчета

D X₁=V₁t₁-a₁t₁²/2;

a₁=F/m=a;

t₁=V₁/a;

D X₁=V₁²/2a;

Тормозной путь второго самолета в подвижной системе отсчета

D X₂’=V₂^’t₂-at₂²/2;

t₂=V₂/a;

D X₂^’=V₂^’2/2a;

D X₂^’=(V₁-V)²/2a;

Мы получили различное перемещение и разное время торможения самолетов и ничего противоестественного в этом нет. Тормозной путь и время торможения самолета при посадке на движущийся авианосец меньше, чем на неподвижном.

Определим теперь перемещение второго самолета в неподвижной системе за время t₁.

D X₂₁^’=V₁t₁-at₂²/2;

D X₂₁^’=V₁²/a-V₂^’2/2a=V₁²/a-(V₁-V)²/2a;

Как видим, за равный промежуток времени самолеты пробегают при торможении в различных системах разную дистанцию по отношению к неподвижной.

Таким образом, динамические процессы перемещения материальных тел в равномерно движущихся с различными скоростями системах отсчета различаются длительностью и протяженностью.

Все бы хорошо, но в замкнутой движущейся системе мы можем пока определять скорость движения самолета только относительно движущегося авианосца. Неподвижный авианосец относится к другой системе отсчета, невидимой с борта второго самолета. А нам надо определить скорость движения или координаты второго самолета относительно и неподвижного авианосца.

Решение напрашивается в поиске какой-то общей системы отсчета, относительно которой могут быть определены координаты обоих самолетов.

В данном примере такой системой отсчета служит Земля. Земля, в этом случае, представляет естественную гравитационную систему отсчета.

Только при наличии третьей(независимой) системы отсчета мы можем определить относительные скорости движения инерциальных систем отсчета.

В этом случае, при посадке самолетов на подвижный и неподвижный авианосцы с равными относительными скоростями, мы должны зафиксировать разные величины затрат энергии на торможение.

Вычисляя затраты энергии в системе отсчета связанной с Землей, мы действительно получаем разные значения.

E₁=mV₁²/2;

E₂=m[(V₁+V)²-V²]/2=m(V₁²+2VV₁)/2;

При вычислении затрат энергии второго самолета в движущейся системе, мы получим равные результаты.

E₂^’=mV₂^’2/2=mV₁²/2=E₁;

Какой же результат соответствует действительности?

Как это ни парадоксально, но оба результата имеют право на существование.

Все зависит от способа торможения.

Если мы будет производить торможение реактивной струей газов, покидающих систему, то верна первая формула, а при торможении упругой связью - вторая.

Для замкнутой системы в процессе всегда будет присутствовать упругая связь. Если реактивная газовая струя остается в системе, то она также будет обладать упругими свойствами.

В этом случае затраты энергии на упругое торможение не будут зависеть от системы отсчета.

Покажем это.

Скорость системы после абсолютно неупругого взаимодействия

V₁₂=(mV₁₁+MV₂₁)/(m +M);

Кинетическая энергия тел до и после взаимодействия

E₁₁=mV₁₁²/2;

E₂₁=MV₂₁²/2;

E₁₂=(M +m)V₁₂²/2=(mV₁₁+MV₂₁)²/2(M +m);

Избыточная, или поглощенная энергия

W=E₁₁+E₂₁-E₁₂;

Рассмотрим вариант, когда массы взаимодействующих тел равны между собой

m =M;

Скорость системы после взаимодействия с неподвижным телом.

V₁₂=mV₁₁/2m=V₁₁/2;

Поглощенная энергия при взаимодействии с неподвижным телом

W₁=E₁₁-E₁₂=mV₁₁²/2-(2m)(V₁₁/2)²/2=mV₁₁²/4;

Скорость системы после взаимодействия с подвижным телом

V₂₂=[m(V₁₁+V)+mV]/(m +m)=(V₁₁+2V)/2;

Поглощенная энергия при взаимодействии с подвижным телом

W₂₂=E₁₁+E₂₁-E₂₂=m(V₁₁+V)²/2+mV²/2-(2m)[(V₁₁+2V)/2]²/2=

=m(V₁₁²+2VV₁₁+2V²)/2-m(V₁₁+2V)²/4=

=(m/4)(2V₁₁²+4VV₁₁+4V²-V₁₁²-4VV₁₁-4V²)=

=mV₁₁²/4;

Как видим, никакой разницы нет.

При посадке самолетов на авианосцы, масса которых многократно превышает массу самолетов, практически вся кинетическая энергия, вычисленная как функция относительной скорости, поглотится в упругих аккумуляторах.

Но пришли мы к этому результату искусственно создав необходимые условия, уравняв относительные скорости самолетов и авианосцев.

При равных скоростях самолетов относительно неподвижной Земли мы получаем совершенно иной результат.

Что же надо сделать для определения скорости движение тел замкнутой системы относительно неподвижной системы отсчета и возможно ли это?

Рассмотрим схему.

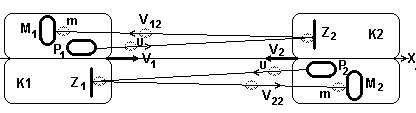
Рис.6

Два одинаковых космических корабля(К1, К2) путешествуют в глубоком космосе.

Между кораблями существует оптическая и радиолокационная связь, позволяющая контролировать относительную скорость и расстояние между ними. Корабли движутся по одной линии с постоянной относительной скоростью U и расстояние между ними постоянно сокращается.

Принцип относительности утверждает, что:

Невозможно определить истинное направление и скорость перемещения центра масс этой системы.
Невозможно определить направление и скорости(V₁, V₂) движения кораблей относительно неподвижной системы отсчета.

Посмотрим, что в действительности можно определить в этой ситуации?

Установим на каждом корабле пушку(), абсолютно упругий отражатель() и абсолютно неупругий приемник-ловушку().

Произведем одновременные выстрелы снарядами, равной массы и обладающими равными относительными скоростями, в направлении другого корабля и посмотрим, что у нас получилось.

Относительная скорость сближения

U=V₁-V₂;

Скорость вылета снаряда из пушки первого корабля в неподвижной системе отсчета

V₁₁=V₁+u;

Скорость вылета снаряда из пушки второго корабля в неподвижной системе отсчета

V₂₁= -(|V₂|+|u|);

для попутного направления

V₂₁= (|V₂| - | u |);

Скорость движения первого снаряда после отражения от абсолютно упругого отражателя, установленного на втором корабле, в неподвижной системе отсчета

V₁₂= -(|V₁₁|+|V₂|)= -(V₁+u+|V₂|);

для попутного направления

V₁₂= -(|V₁₁|-|V₂|)= -(V₁+u-|V₂|);

Скорость движения второго снаряда после отражения от абсолютно упругого отражателя, установленного на первом корабле, в неподвижной системе отсчета

V₂₂=V₁+|V₂₁|=V₁+|V₂|+|u| ;

для попутного направления

V₂₂=V₁+|V₂₁|=V₁-|V₂|+|u| ;

Можно заметить, что скорости снарядов и их импульсы равны по величине и противоположны по направлению. Импульс сил упругих деформаций преобразовался в импульс движения снарядов в полном соответствии с законами сохранения. Но при этом они движутся навстречу кораблям, обладающих разными скоростями.

Относительная скорость встречи первого снаряда с первым кораблем

U₁=V₁-V₁₂=2V₁+ u+|V₂|;

для попутного направления

U₁=V₁-V₁₂=2V₁+ u-|V₂|;

Относительная скорость встречи второго снаряда со вторым кораблем

U₂=V₂₂-V₂= V₁+2|V₂|+| u | ;

для попутного направления

U₂=V₂₂-V₂= V₁-2|V₂|+| u | ;

Мы получили систему из двух уравнений. Решим ее относительно скоростей движения кораблей в неподвижной системе отсчета

|V₂|=U₁-2V₁- u;

|V₂|= -U₁+2V₁+ u;

U₂=V₁+2U₁-4V₁- 2u +u;

U₂= V₁+2 U₁-4V₁- u;

U₂=2U₁-3V₁-u;

U₂=2U₁-3V₁-u;

V₁=(2U₁-U₂-u)/3;

V₁=(2U₁-U₂-u)/3;

|V₂|= U₁-2[(2U₁-U₂-u)/3]- u;

|V₂|= -U₁+2[(2U₁-U₂-u)/3]+ u;

|V₂|= (-U₁+2U₂-u)/3;

|V₂|= (U₁-2U₂+u)/3;

Относительные скорости движения снарядов и кораблей могут быть измерены обычными способами радиолокации.

Скорость движения первого корабля в неподвижной системе отсчета

V₁=(2U₁-U₂-u)/3;

Скорость движения второго корабля в неподвижной системе отсчета

V₂= -(2U₂-U₁-u)/3;

Скорость движения центра масс системы из двух кораблей в неподвижной системе отсчета

V₀=(V₁+V₂)/2=(2U₁-U₂-u-2U₂+U₁+u)/6;

V₀=(U₁-U₂)/2;

Таким образом, мы преодолели все запреты принципа относительности и определили скорость движения кораблей и центра масс замкнутой системы относительно неподвижной системы отсчета.

Все бы хорошо, но встает вопрос, относительно какой “неподвижной” системы отсчета будут определены эти скорости?

Допустим, что корабли находятся на границе сферы гравитационного влияния Земли.

Какую скорость мы определим в этом случае? Что будет являться системой отсчета, Земля, Солнце, центр Галактики или абсолютный центр Вселенной?

Вышеприведенные формулы не могут дать ответ на этот вопрос. Почему?

Потому, что нет привязки энергетических процессов к конкретным свойствам данной области пространства, определяемых его гравитационным потенциалом.

Кроме всего прочего, принцип относительности предполагает, что преобразование потенциальной энергии в кинетическую не зависит от гравитационных свойств пространства. В данном случае речь идет не о преодолении сил гравитации в радиальном направлении, которые изменяются при переходе от одного небесного объекта(планеты, звезды и т.д.) к другому в соответствии с законом всемирного тяготения, а о движении в гравитационном поясе пространства постоянного радиуса.

Это, например, относится к процессам движения по поверхности различных планет.

Существующая теория предполагает, что механическая система из пружины и, закрепленных на ее концах, шариков, равной массы, будет вести себя в любой точке пространства одинаково.

Если две такие системы одновременно привести в колебание, например, на Земле и Марсе, то, без учета трения, мы должны наблюдать полностью синхронные процессы.

Колебания должны происходить в плоскости, растекающейся под действием гравитационных сил жидкости, что будет соответствовать постоянству гравитационного радиуса, а не в геометрической плоскости. Это исключит возможность увязать возникающие рассогласования в колебаниях с влиянием радиальной составляющей гравитационных сил.

В настоящее время не существует алгоритма, способного показать, что при этих условиях мы будем наблюдать рассогласование в процессах колебания одинаковых систем, установленных на разных планетах.

Отсутствие такого алгоритма позволило родиться абстрактным математическим утверждениям об инвариантности физических систем отсчета, определяемых естественными гравитационными свойствами данной области пространства.

Вне связи с гравитационными характеристиками пространства, инерционные свойства материи просто теряют свою физическую сущность.

Не зря до сих пор никому не удалось разделить физически инерционную и гравитационную массы. Существует просто масса, без всяких приставок и заключает она в себе количественные характеристики материи и не надо издеваться над философскими категориями. Масса двух кирпичей всегда будет в два раза выше массы одного, но никак не в три или в четыре.

Если мы воспринимаем тот факт, что ускорение свободного падения имеют разные величины на разных планетах, что влечет с собой различные энергетические затраты на перемещение в радиальном направлении, то почему бы не воспринять и тот факт, что равные импульсы сил, приложенные к равным телам на разных планетах в горизонтальном направлении, могут приводить к подобным эффектам и одинаковые пружинные маятники будут колебаться с различной частотой и амплитудой.

В этом случае у нас исчезает неопределенность в привязке к системам отсчета.

Скорость космических аппаратов будет определятся относительно массивного гравитационного объекта, в сфере влияния которого они находятся.

Относительная скорость снарядов, вылетающих из пушек, будет изменяться пропорционально гравитационному потенциалу в данной точке пространства.

Если мы сравним результаты определения скорости движения подводных лодок, космических кораблей на околоземной и гелиоцентрической орбитах, то сможем увидеть разницу в энергетических затратах при стрельбе из пушек.