| О нас | Физика и техника | Философия | УФО-логия | Астрология | Медицина | Прочее | Конференции | Каpта Сайта | Поиск |
| О нас | Физика и техника | Философия | УФО-логия | Астрология | Медицина | Прочее | Конференции | Каpта Сайта | Поиск |

ВВЕДЕНИЕ
Принцип относительности, сформулированный еще Галилеем и нашедший свое продолжение в работах Ньютона и Эйнштейна, все чаще начинает оспариваться специалистами в области электродинамики и физики высоких энергий, но никто не хочет видеть явное нарушение этого принципа при полетах воздушных и космических летательных аппаратов.
Считается, что параметры работы механизмов и систем летательных аппаратов не зависят от скорости их полета, но многочисленные “непонятные” аварии, происходящие при определенных режимах полетов, заставляют задуматься над этим утверждением.
Очень показательным примером в этом отношении является история создания винтокрыла Ка-22 (http://avia.russian.ee/helix/russia/ka-22.html)
..."Винтокрыл
во многом вторгался в область
неизведанного. И дело было не
только в огромных габаритах.
Несущие винты этого летательного
аппарата
(концы лопастей) на максимальных
оборотах при малом шаге почти
достигали
скорости звука. И это ему не
нравилось. Нагрузка на лопасть была
45кг/м2 (у
вертолета лишь порядка 18-20кг/м2).
Ниже располагалось самолетное
крыло с
расчетным профилем, значительно
снимавшее нагрузку на винты в
горизонтальном
полете, однако сверху на него на
режиме висения давила струя от
несущих
винтов (это тоже не нравилось
Камову). Чтобы уменьшить этот
"вредный обдув",
в крыло встроили по всей длине
закрылки, отклонявшиеся на 90
градусов; они
существенно уменьшали потери и
улучшали аэродинамику.
Однажды в испытуемом узле срезало
все болты на больших оборотах и они,
как
картечный залп, ударили по стенам
цеха лаборатории, чудом никого не
убив.
Дефект устранили, изменив
конструкцию, но Николай Ильич
долгое время не мог
успокоиться.
- Надо думать, думать, думать, -
говорил Камов молодым и
старым, -
недостаточно владеть авиационной
наукой, нужно также уметь ею
пользоваться.
Конечно, вещи невиданные, скрытые и
непознанные порождают и страх. Но
мы
должны думать и действовать.
Наконец, полоса лабораторных
"погнуток" кончилась, все
агрегаты работали
безотказно. 17 июня 1959 года был
назначен первый полет винтокрыла.
Летчиками-испытателями утверждены
Дмитрий Ефремов и Олег Яркий.
Первый полет винтокрыла, согласно
заданию в полетном листе, был на
"зависание" в метре над землей,
затем в двух, трех и так до пяти
метров над
полем аэродрома. Летчику
предстояло выяснить и
почувствовать: какова
продольная и поперечная
управляемость, насколько
эффективны рули и, конечно,
проверить работу двигателей и
прочих агрегатов.
В этот день зависание
длилось
всего несколько секунд. Ефремов
очень быстро
уловил неустойчивость и "путевое
рысканье", что было опасно. Он
мягко
опустил винтокрыл на землю, подумал
и через некоторое время вновь завис
на
метре - рысканье повторилось. Это
увидел и Камов с земли. Машину
поставили в
цех.
Испытания продолжались. В одном из
полетов над аэродромом оторвалась
лопасть
несущего винта. Винтокрыл стало
немилосердно трясти из-за
дисбаланса сил, но
Ефремов успел уменьшить обороты и
произвел посадку
"по-самолетному".
В короткий срок молодой инженер
Женя Пак сконструировал из разных
материалов
(что было новинкой!) прочнейшую
эластичную лопасть. И винтокрыл,
будучи
красавцем, стал хорошо летать,
оглашая окрестности свистящим
шумом турбин.
Наконец, дела в КБ пошли успешно.
Работа спорилась,
приступили к завершающим
ресурсным испытаниям. Благодаря
новой технологии в изготовлении
лопастей,
придуманной молодым инженером
Евгением Паком, ресурс увеличился
примерно в
300 раз! (У первых ресурс был всего 12
часов.)
Правда, на изготовление одной
такой многослойной лопасти уходило
2 месяца,
но зато она превосходно работала!
Услышав о таком "чуде", М.Л.Миль
(недавний ученик Камова) прислал
своих
технологов для перенятая опыта. И
хотя с этой "фирмой" отношения
были
натянутыми или, лучше сказать,
"холодноватыми" (Миль и его
замы подчас за
глаза хулили в Минавиапроме работу
КБ Камова), Николай Ильич, помахав
тюбетейкой, как веером, со вздохом
сказал:
- Валяйте, перенимайте опыт!..
Ресурс лопастей несущего винта на
вертолетах Миля скоро резко возрос,
но в
отчетах изобретателем новой
технологии был назван другой
инженер. Камов не
обижался, ибо был великодушным, как
всякий талантливый человек.
В одном из полетов Юрия Гарнаева на
винтокрыле разрушился передний
подшипник
двигателя. Двигатель без лишних слов
заменили, прислав с завода новый.
Причина разрушения была не совсем
ясна. Испытания продолжили, а о
поломке
постарались забыть, хотя Камов
несколько раз пытался у заводских
двигателистов выяснить результат
исследований. Ответ всякий раз был
неопределенным: может, то, а может, и
совсем другое. (Впоследствии это
стало
предлогом для запрета темы.)
Два винтокрыла, которые перегнали
на московский аэродром, хорошо
летали, и
испытания шли успешно. 14 сентября
1962 года Камову исполнялось 60 лет, и
в
КБ готовились отметить круглую
дату.
Но юбилей был испорчен. В один из
дней винтокрыл возвращался с
длительного
перелета. При снижении на посадку
прямо над взлетно-посадочной
полосой его
вдруг стало резко разворачивать,
затем накренило почти на 90
градусов, и он
рухнул. При ударе о землю машина
разрушилась, а весь экипаж вместе с
шеф-пилотом Дмитрием Ефремовым
погиб. Это было страшным
потрясением для
всех.
Точно установить причину
катастрофы государственной
комиссии не удалось, но
было похоже, что произошел отказ
управления.
Камов сделал управление жестким,
заменив тросы на тяги. Испытания
продолжились.
Ровно через два года - 5 сентября 1964
года - снова катастрофа, очень
похожая на первую.
Как рассказывали очевидцы, первый
полет в этот раз прошел без
замечаний.
В 7 часов 30 минут
винтокрыл вторично взлетел. Первым
пилотом был Боровцев,
вторым Гарнаев. Винтокрыл набрал
высоту 100 метров, сделал круг, и
вдруг его
стало переворачивать на спину и
затем затягивать в пикирование.
Экипажу удалось вывести винтокрыл
в горизонтальный полет, как вдруг
оторвалась гондола.
Трое успели выброситься на
парашюте, в том числе и Юрий Гарнаев
(он когда-то
испытывал первые катапульта), а
Боровцев и инженер КБ Рогов не
успели.
Винтокрыл упал у железнодорожного
полотна перед идущей электричкой.
Боровцев
явно до конца старался удержать
винтокрыл от падения на эту
электричку.
Николай Ильич осунулся, постарел.
Работу над винтокрылом приказали
закрыть.
Доказать начальству, что винтокрыл
перспективная, нужная машина с
уникальными качествами, не удалось.
В США же работы над конвертопланом,
весьма похожим на винтокрыл Ка-22,
продолжили и "доводили" его
целых 30 лет.
Сейчас у них имеется надежный
аппарат XV-22. Неудач при этом было
предостаточно. Примерно в те же
годы, что и у нас, произошли две
катастрофы,
которые тем не менее не
обескуражили американцев, и решено
было после
устранения причин катастрофы
продолжить испытания, сосредоточив
все внимание
на системе управления и
аэродинамике, которая, как
оказалось, чрезвычайно
сложна и изобилует различными
эффектами, включая и "прилипание
воздушной
струи к поверхности крыла, а также
сдув пограничного слоя и
турбулентность".
Камов еще некоторое время пытался
возродить тему винтокрыла, в КБ
были
разработаны улучшенные эскизные
проекты, но их не одобрили.
А.П.Маслов и военный
вертолетчик Г.Н.Мдивани говорили,
что Камов мечтал
вернуться к винтокрылу.
Конструктор говорил, что причина
катастроф с Ка-22 -
малоизученная аэродинамика. Важно
было подобрать винты нужного
диаметра (как
это сделали американцы). И еще он
рассчитывал побороть
недоброжелательность
и зависть в Минавиапроме, не давшие
ему осуществить задуманное..."
Действительные причины
многочисленных “отказов”
механических систем этой
уникальной конструкции так и не
были найдены.
Какие неизвестные силы отрывают лопасти винтов, разрушают опорные подшипники, приводят к “непредсказуемому” поведению летательного аппарата?
Причина всех этих явлений одна - неправомерность распространения “принципа относительности” на реальные механические системы.
1. ТЕОРИЯ
Со времен Галилея, принцип относительности существует как незыблемый постулат механики. Но, что такое принцип относительности и можно ли ему доверять в эпоху космических полетов?
Математически принцип относительности Галилея сводится к преобразованию координат идеализированной системы отсчета, находящейся вне сферы действия гравитационных полей. При этом правильно утверждается, что, при выбранных условиях, за равные промежутки времени движущееся тело будет проходить равные отрезки в обеих системах отсчета.
xA' = xA - xO' = xA - V·t; (1)
Dx' = |xB' - xA'| = |(xB - V·t) - (xA - V·t)| = Dx. (2)
Но мы живем в мире гравитации, а не в мире математических иллюзий и должны все процессы рассматривать в системах отсчета, привязанных к естественным гравитационным объектам.
Ниже изображены две системы отсчета, движущиеся с постоянной скоростью, но первая состоит из двух автомобилей, движущихся по поверхности Земли, а вторая - из двух КЛА, движущихся на орбитах ИСЗ.
Принцип относительности утверждает, что все процессы в данных системах будут протекать одинаково.


Рис.2 Рис.3
Но это утверждение неправомочно для систем, находящихся в различных гравитационных полях, и мы постараемся это наглядно доказать.
Красный автомобиль, обгоняя синий, движущийся с постоянной скоростью относительно неподвижной Земли, затратит определенное количество энергии, определяемое выражением
W=E2-E1=M(V22-V12)/2=M[(V+U)2-V2]/2=MU(V+U/2); (3)
Удельный расход энергии на изменение скорости движения красного автомобиля относительно синего
q =U(V+U/2); (4)
зависит как от относительной скорости автомобилей, так и от скорости движения синего автомобиля относительно неподвижной Земли.
Приняв в качестве локальной системы отсчета синий автомобиль, мы не вправе утверждать об инвариантности подобных систем отсчета, движущихся с различными скоростями относительно Земли, так как расход энергии для относительного изменения скорости красного автомобиля на одну и ту же величину будет во всех таких системах разным.
Будем постепенно увеличивать скорость движения синего автомобиля относительно Земли и доведем ее до первой космической, то есть превратим автомобиль в КЛА, движущийся по круговой орбите ИСЗ (Рис.3).
Следовало бы ожидать, что удельный расход энергии разгона будет определяться выражением
q0 =U(Vk+U/2); (5)
но из практики космических полетов известно, что он равен
q0U =U2/2; (6)
У нас исчезла зависимость удельного расхода энергии разгона от скорости движения локальной системы отсчета относительно неподвижной.
Перенеся этот результат на все движущиеся локальные системы отсчета, мы получаем принцип относительности.
Но не будем останавливаться, и увеличим скорость нашей локальной системы отсчета (синего космического корабля). Начинается как бы новый отсчет, где круговая скорость является нулевой точкой.
Удельная энергия разгона опять будет зависеть как от относительной, так и от, превышающей круговую, скорости движения локальной системы отсчета
q0V=U[(V-VK)+U/2]; (7)
Но, при движении системы отсчета (синего КЛА) со второй космической скоростью, он выйдет из сферы гравитационного действия Земли и превратится в искусственную планету, обращающуюся вокруг Солнца со скоростью движения Земли. Расход удельной энергии разгона красного КЛА опять будет определяться только относительной скоростью. И так будет продолжаться до тех пор, пока мы не перейдем в систему центра масс Вселенной.
Можно представить зависимость удельной энергии разгона от скорости движения локальной системы отсчета относительно гравитационного объекта в виде следующего графика

Рис.4
На рис.4 изображен упрощенный вариант зависимости изменения удельной энергии разгона в гравитационном поле планеты от скорости движения системы отсчета. На оси Х представлены значения удельной энергии в условных единицах, а на оси Y - значения скорости движения системы отсчета.
Как видим, в реальном материальном мире принцип относительности не может существовать.
Принцип относительности существует, как математическая абстракция в нереальном пространстве, лишенном гравитации.
Можно отметить, что исключение гравитации приводит к потере физической сущности движения материальных тел.
Исключение массы, как основного атрибута гравитации, из процесса описания движения также приводит к абсурдным результатам.
Представим, что мы определили затраты энергии на изменение скорости движения кораблей в “пустом пространстве”.
Очевидно, что в таком случае любое изменение скорости не должно сопровождаться потреблением энергии??!!!
Рассмотрим это в отношении кораблей, находящихся на околоземной орбите. Пусть они находятся на высокой круговой орбите. Нам надо увеличить эту скорость на 1 км/сек. Затраты энергии в этом случае будут определяться только массой Земли и расстоянием между ней и кораблем.
Будем “уменьшать” массу Земли!!!
Естественно станет уменьшаться и расход энергии.
При массе Земли равной нулю мы получим нулевой расход энергии!!!
Можно вдобавок рассмотреть в этом примере и параметры изменения орбиты, получится очень интересный результат.
Подобный процесс можно воспроизвести в лабораторных условиях, заменив гравитацию электромагнитными силами.
Этот пример доказывает неправомерность рассмотрения физических процессов вне сферы действия гравитационных сил.
Движение замкнутой системы материальных тел можно рассматривать только при наличии гравитационного поля.
Взаимосвязь массы и энергии в процессе взаимодействия материальных тел можно показать на следующем примере.

Рис.5
В качестве примера зависимости внутренней энергии пружины от массы можно привести парадоксальное исчезновение энергии при отсутствии массы.
Возьмем обыкновенную пружину, растянем ее и отпустим. В какую работу преобразуется потенциальная энергия растянутой пружины? Ответ однозначен - в работу по перемещению ограничивающих связей.
Теперь несколько изменим эксперимент.
Установим сжатую пружину между двумя тележками равной массы (Рис.5a). В пружине произойдет накопление потенциальной энергии. Свяжем пружину нитью, то есть наложим ограничивающую связь. Перережем нить. Энергия пружины начнет преобразовываться в кинетическую энергию движения тележек (Рис.5b). Пройдя нулевую отметку упругого состояния, пружина начнет растягиваться. Кинетическая энергия тележек вновь будет преобразовываться в потенциальную энергию растянутой пружины. В момент остановки тележек вся их кинетическая энергия преобразуется в потенциальную энергию пружины (Рис5с). Обрежем в этот момент связи между пружиной и тележками. Тележки останутся неподвижными, а пружина начнет сжиматься. После совершения нескольких колебательных движений, пружина остановится в своем нейтральном положении.
Масса пружины во много раз меньше массы тележек и потери на внутреннее трение, при ее свободном колебании, можно считать равными нулю.
Потенциальная энергия растянутой пружины определяется квадратом удлинения
P=kx2/2; (8)
Куда исчезает эта энергия при разрыве связей с массивными тележками?
Она перестает существовать?!
А может тележки “мгновенно” изменят скорость и приобретут кинетическую энергию?
Но этого не должно быть, так как их скорость в момент разрыва связей равна нулю, а силы действия пружины направлены внутрь системы.
В то же время, исходя из третьего закона Ньютона, силы действия пружины должны быть уравновешены другой, противоположной по направлению. Это будут силы инерции “ускоряющихся” шаров, которые могут существовать только при наличие упругих связей, но мы разрываем эту связь. Ускорения шаров нет, а, значит, нет и сил инерции. Отсутствие сил инерции должно сопровождаться отсутствием и сил упругой деформации?
Третий закон Ньютона нельзя применять к движущимся системам, так как он отражает уравновешенное статическое состояние, а любое движение вызывается именно разностью действующих сил. Книга, лежащая на столе, начнет перемещаться только тогда, когда мы приложим к ней силу, превышающую силу трения. При наличии постоянной преобладающей силы, тело будет ускоряться.
Работа (преобразование энергии) определяется действием силы на участке линейного перемещения.
A = Fx =(ma)x (9)
При отсутствии в формуле хотя бы одной величины, преобразования энергии не будет.
Итак, мы поставили под сомнение два элемента классической механики - принцип относительности и третий закон Ньютона в применении к движущимся системам.
Теперь нам ничто не мешает усомниться и в справедливости закона сохранения импульса, доказательство которого построено на принципе относительности и третьем законе Ньютона.
Закон сохранения энергии, который невозможно отменить, не обязывает механическую систему подчиняться закону сохранения импульса. Принципиально, закон сохранения энергии дает возможность преобразовать внутреннюю(потенциальную) энергию системы в кинетическую энергию направленного движения, но закон сохранения импульса и принцип относительности запрещают подобный процесс.
Закон сохранения импульса накладывает на систему ограничения, которые можно записать в виде
i m1V1i +i m2V2i =2Ft; (10)
E1= m1V12/2; E2= m2V22/2; (11)
m1V12/2+m2V22/2=W; (12)
W =q(m1+m2); (13)
E1=qm2; E2=qm1; (14)
W- подведенная потенциальная энергия;
E1, E2- кинетическая энергия тел после подведения потенциальной;
Ft- импульс упругих сил;
i m1V1i ,i m2V2i - импульс (количество движения) после подведения упругой энергии;
q-удельная потенциальная энергия, подведенная к системе.
Но закон сохранения энергии будет выполняться и в том случае, если распределение энергии источника между взаимодействующими телами будет происходить в какой-то зависимости от параметров движения. Общий вид такой зависимости можно представить в виде
E1=q(1-K)m2/2; (15)
E2=qm2+q(1+K)m2/2; (16)
E1+E2= q(1-K)m2/2+qm1+q(1+K)m2/2=q(m1+m2)=W; (17)
K =f(V, V0, q); (18)
K -коэффициент, изменяющийся от 0 до 1 и функционально зависящий от гравитационных параметров данной области пространства, скорости движения системы относительно гравитационного центра масс и удельной энергии, подводимой к телам системы.
Как видим, распределение энергии между телами механической системы может очень сильно отличаться от принятого.
На основании этого материала вполне можно допустить, что импульс упругих сил распределяется между движущимися телами неравномерно, что можно проиллюстрировать на примере с движущимися автомобилями, расталкиваемыми пружиной.

Рис.6
В этом случае энергия пружины, необходимая для разгона красного автомобиля определится, как квадрат разности скоростей
D E=M(V2-V1)2/; (19)
При непосредственном разгоне автомобиля, чем больше будет его начальная скорость, тем больше энергии потребуется на подобное увеличение, расход энергии в этом случае определяется как разность конечной и начальной кинетической энергии и пропорционален разности квадратов конечной и начальной скоростей
D E=E2-E1=M(V22-V12)/2; (20)
При этом мы можем использовать как колесный, так и реактивный движитель, результат не изменится.
В первом случае два автомобиля будут представлять замкнутую систему с общим центром масс. При этом, приобретенные ими импульсы не будут равны между собой. Подобный эксперимент можно поставить в лабораторных условиях, используя вместо автомобилей небольшие тележки

Рис.7
При определенных условиях проведения эксперимента и наличии точного измерительного оборудования, мы можем зафиксировать разницу приобретаемых импульсов.
При динамическом взаимодействии объектов в движущейся замкнутой системе материальных тел появляется неуравновешенный импульс, вызывающий изменение скорости движения центра масс системы.
Величина неуравновешенного импульса зависит от гравитационного потенциала области пространства, в которой находится движущаяся система, ее скорости относительно гравитационного объекта и удельной энергии, подводимой при взаимодействии.
В тоже время, в космических полетах это явление проявляется в виде многочисленных аварий КЛА и их механических систем. Особенно заметно это стало при полетах к Марсу и кометам, когда по непонятным причинам во время проведения обычных маневров стали пропадать самые совершенные космические аппараты.
Явление неуравновешенного импульса наблюдается повсеместно и в Земных условиях, но его значения теряются в инертности практического мышления, которое не замечает очень многих явлений не связанных с непосредственным получением выгоды. А ведь неуравновешенный импульс позволяет: спортсменам устанавливать мировые рекорды; земноводным совершать невероятные прыжки; рыбам и животным передвигаться с большой скоростью.
Неуравновешенный импульс очень влияет на расход топлива летательных аппаратов. Неуравновешенный импульс проявляется в “непонятных” катастрофах вертолетов и самолетов, тысячах автомобильных аварий, постоянно происходящих на дорогах планеты.
Практически, неуравновешенный импульс проявляется во всех сферах нашей жизни - от работы сердца, до космических полетов, но мы упорно ничего не хотим замечать.
2. ПРЕДИСТОРИЯ ЭКСПЕРИМЕНТА
Эксперимент поставлен по материалам автора в г. Красноярске группой энтузиастов в составе Н.П. Шестакова, Ф.В. Марьясова, А. Иваненко.
Зарегистрировать положительные результаты удалось благодаря методике определения скорости вращения маховика, разработанной Н.П. Шестаковым и А. Иваненко, а изготовить устройство только благодаря настойчивости Ф.В. Марьясова.
Следует отметить, что данному эксперименту предшествовал анализ причин аварии американских КЛА в 1999 г., происшедших при попытке посадки на поверхность Марса, выполненный автором по материалам НАСА.
Анализ работы акселерометров, установленных на американских КЛА для определения плотности атмосферы Марса, показал, что их данные не могут быть объяснены только свойствами атмосферы. На одной и той же высоте акселерометр показывал совершенно разные значения .
От орбиты к орбите акселерометр показывал довольно странную зависимость.

То же самое происходило и при изменении угла наклона орбиты.

Специалисты НАСА отнесли подобный разброс показаний акселерометра MPL за счет сплюснутости Марса, пылевых бурь и перепада температур, но посмотрим на поведение другого Марсианского спутника - MGS, который до сих пор находится на околокруговой орбите с очень малым эксцентриситетом.
Скорость движения КЛА в нижней точке орбиты изменяется от оборота к обороту также “странным” образом, объяснить который невозможно никакими известными видами прецессии.
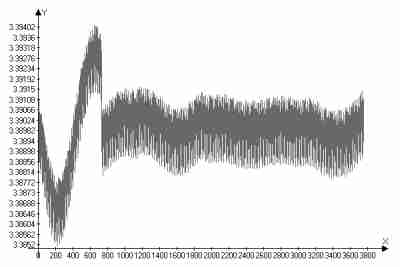
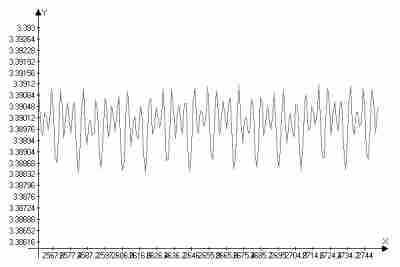
В увеличенном масштабе график изменения скорости очень напоминает показания работы акселерометра. Но этот спутник движется на высоте около 400 км над поверхностью Марса и ни о каком влиянии атмосферы не может идти речь.
Следовало задуматься над причинами такого поведения КЛА.
Автором было высказано предположение, что причиной такого поведения КЛА является “неуравновешенный импульс”, возникающий в замкнутой системе, движущейся относительно гравитационного объекта, то есть подтверждались теоретические предпосылки существования такого процесса.
Амплитуда изменения параметров на всех графиках сравнительно мала и зарегистрировать ее стало возможным только с применением высокоточных измерительных приборов.
Для окончательного ответа требовалось провести эксперимент в Земных условиях.
Основным требованием для его проведения была высокая точность измерительной аппаратуры и автором был предпринят поиск создателей точных измерительных устройств.
Такой специалист (Шестаков Н.П.) оказался в Красноярском ИФ СО РАН, в городе, где не только занимаются точными измерениями, но разработкой и запуском самих спутников, что и явилось основным критерием для проведения эксперимента.
Благодаря усилиям представителя автора в Красноярске Ф.В. Марьясова, удалось создать рабочую группу по проведению эксперимента.
3. ЭКСПЕРИМЕНТ -ГДС_01
ПРОВЕРКА ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
ДЛЯ МЕХАНИЧЕСКИХ СИСТЕМ
С.Н. Шмидт, Н.П. Шестаков, Ф.В. Марьясов, А. Иваненко
ПОСТАНОВКА ЗАДАЧИ
Сравнение показателей работы механической и математической моделей замкнутой системы с целью выявления влияния поступательной скорости системы на параметры движения ее элементов.
СХЕМА ЭКСПЕРИМЕНТА
Устройство состоит из вентилятора, турбины с, закрепленной на ее оси, штангой с грузиком и системы электронно-оптического измерения скорости вращения турбинного колеса.
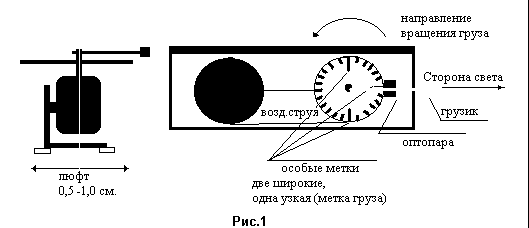
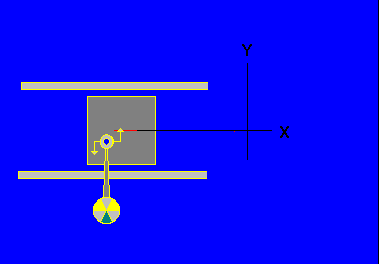
Рис. 2
Математическое моделирование выполнено в программе “Универсальный механизм”.
К телу 1, перемещающемуся в поступательном шарнире относительно системы отсчета, присоединен, через вращающийся шарнир, маятник. Во вращающемся шарнире создаются активный и реактивный моменты.
Принцип относительности утверждает, что характер вращения маятника не зависит от скорости перемещения системы (тело1).
Программа использует общепринятые законы классической механики и полностью “подтверждает” принцип относительности.
На нижеследующих графиках представлено движение маятника для неподвижного и движущегося тела 1.
Изменение скорости движения системы математической модели, не приводит ни к каким изменениям окружной скорости маятника.
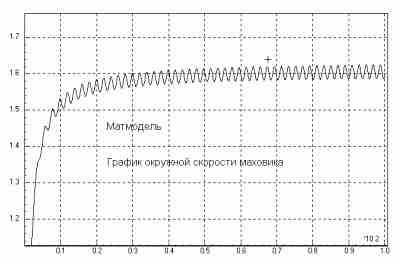
Рис. 3 Система покоится.

Рис. 4 Система движется.

Рис. 5
В то же время, измерения скорости вращения турбины механической модели однозначно показывают ее зависимость от скорости поступательного движения устройства.
На этом графике представлены параметры вращения турбины при различной скорости движения автомобиля - подвижная лаборатория.
Измерения проводились в прямом (С-З, тонкие линии) и обратном (Ю-В, толстые линии) направлении движения автомобиля.
Общий характер графика изменения скорости вращения турбины при движении автомобиля совпадает с графиком движения спутника.

ВЫВОДЫ:
4. ПРИКЛАДНОЕ ЗНАЧЕНИЕ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА
1. Результаты эксперимента позволяют сделать вывод о том, что на лопасти несущих винтов вертолета и лопатки турбин авиационных двигателей, помимо аэродинамических сил, действуют НЕИЗВЕСТНЫЕ ДИНАМИЧЕСКИЕ СИЛЫ.
Рассмотрим подробнее это воздействие на винт вертолета.

Эксперимент показывает, что на каждую лопасть несущего винта в текущий момент времени будут действовать разные по величине ДИНАМИЧЕСКИЕ МОМЕНТЫ. При вращении винта, величина и направление динамического момента изменяются нелинейным образом.
Величина динамического момента зависит от скорости вращения винта и скорости горизонтального полета. В режиме “зависания” действует фактор скорости вращения Земли.
Динамические моменты придают несущему винту “дисбаланс”, который влечет за собой образование опрокидывающих моментов, разрушающих напряжений и “резонансной вибрации”.
Величина пиковых значений динамических моментов может многократно превосходить аэродинамическое сопротивление.
Пиковые напряжения возникают при различных сочетаниях окружной и линейной скоростей, а также зависят и от других параметров.
В аэродинамической трубе невозможно воспроизвести подобный процесс.
Можно сделать вывод, что все аварийные ситуации в истории создания Ка-22 и многие “непонятные” аварии других летательных аппаратов вызваны НЕУРАВНОВЕШЕННЫМ ИМПУЛЬСОМ.
2. Эксперимент свидетельствует о возможности создания навигационных приборов принципиально нового типа, основанных на регистрации неуравновешенного импульса.
Кострома - Красноярск, 2000 г.
Комментарий